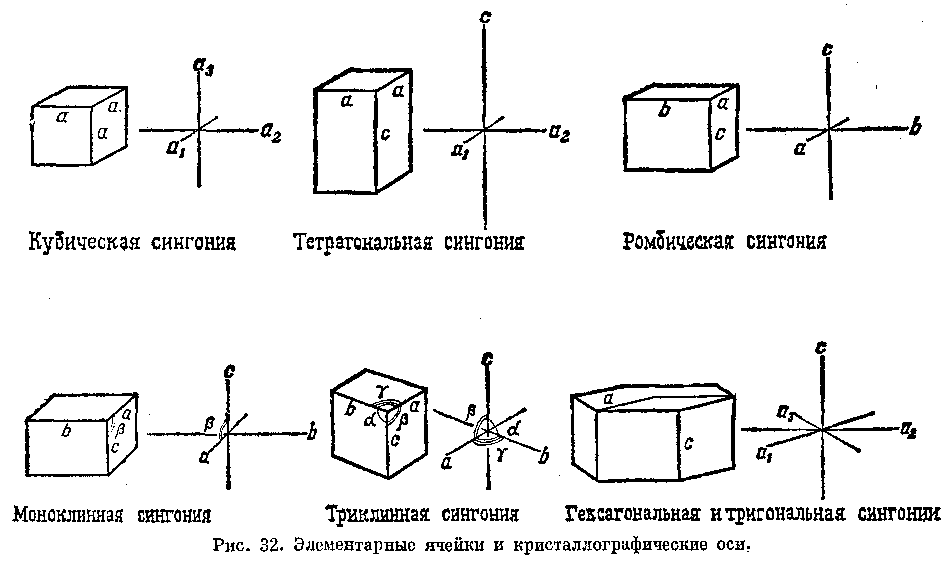
Для цілей опису положення кожної грані на поверхні кристала приводиться до системи трьох прямі ліній, що перетинаються на початку координат, так само як це робиться в геометрії. Ці прямі лінії називаються кристалографічними осями. Перше ніж стало можливим вивчати внутрішню структуру кристалів безпосередньо, за допомогою рентгенівських променів, положення цих осей визначалося по зовнішній морфології. Простіше всього ці осі можна собі представити в об`ємних «одиничних гніздах», з яких, як тепер відомо, і побудовані всі кристали (мал. 32).
У кубічній сингонії кристалографічні осі — це. система трьох рівних відрізків а*, а
, а
, паралельних ребрам одиничного куба й розташованих під прямими кутами. У тетрагональній сингонії елементарне гніздо — пряма призма квадратного перетину; кристалографічні осі знову розташовуються під прямими кутами, але вертикальна вісь із (паралельна четверной осі симетрії) відрізняється по довжині від однакових горизонтальних відрізків aj, а
. Осьове відношення с/а визначається як відношення довжин сторін елементарного гнізда; так, v циркону
У ромбічній сингонії елементарне гніздо — це прямокутний паралелепіпед з різними по величині відрізками а, Ь, з, паралельними трьом подвійним осям симетрії й також розташованими під прямими кутами. У топазу а=4,650, 6=8,800, з=8,394, осьове відношення а/b : 1 s c/b рівно 0,528 s 1 i 0,954.
У моноклінних кристалах структура така, що вибрати елементарне гніздо, у якому осі розташовуються під прямими кутами, уже не можна. Гніздо тут являє собою похилу призму, що умовно міститься так, щоб вісь а виявилася нахиленої убік спостерігача вниз, утворюючи в площині симетрії кут Р>90° з вертикальною віссю з; кристалографічна вісь Ъ паралельна подвійної осі симетрії й, отже, перпендикулярна площині, що містить осі а й с. У диопсида а ~ =9,73, 6=8,91, з=5,25, р = 105°50, а в сфену а=6,56, Ь-Ь—8,72, з=7,44, р = 119°43.
У кристалах, що ставляться до триклинної сингонії, осей, що йдуть під прямими кутами, немає й кристалографічні осі розташовуються неправильно; три нерівні осі а, Ь, з нахилені ДРУГ до друга під кутами а, (5, в, жоден з яких не рівний 90. Кристалографічні параметри аксинита: а=7,15, Ь= =9,16, з=9,86, а=88°4 р=81°36,
в=77
42.
У гексагональній і тригональної сингоніях виявилося зручним використовувати систему чотирьох кристалографічних осей:
трьох горизонтальних осей а±, а
, а
, розташованих під кутами 120° друг до друга, і вертикальної осі з, перпендикулярної площини, що містить перші три осі (отже, вісь із паралельна шестерної або потрійної осі симетрії).
Для позначення взаємного розташування граней по відносин до кристалографічних осей використовується система індексів граней, або символів Міллера
( на прізвище Вільяма Хєл-Лоуза Міллера, 1801-1880). Площина, що відтинає від кристалографічних осей відрізки, що співвідносяться між собою як ребра елементарного гнізда а, Ь, з, називається одиничною площиною. Якщо ці ребра однакові, то індекс записується 111 (читається: «один — один — один»). Індекс будь-який інший грані кристала записується (hkl), де alh, Ик, ell — відрізки, що відтинаються цієї гранню на трьох осях (мал. 33).
Таким чином, щоб визначити індекс якої-небудь грані, треба розділити параметричні відрізки на відрізки, що відтинаються цієї гранню, скорочуючи, якщо потрібно, дроби. Ми згадали вище, що в топазу а : Ъ : з=0,528 : 1:0,954; виявлене, що дві інші грані, що часто зустрічаються, нахилені так, що вони відтинають відрізки з осьовими відносинами 0,528 : 1:0,477 і оо : 1:1,918. Отже, індекси цих граней будуть наступними:
Той факт, що в кристалах усіх симетрій існують такі прості співвідношення, дозволив сформулювати запою раціональності індексів (індекси граней можна виразити невеликими
цілими числами або нулем). Із цього закону випливають важливі висновки, що стосуються характеру внутрішньої структури кристалів; ці висновки повністю підтвердилися потім при рентгеноскопії кристалів
Відрізок, що відтинається на негативному продовженні осі, позначається рисою над відповідною цифрою; так, індекс передньої нижньої правої грані октаєдра (мал. 34) — (111) (читається: «один — один — мінус один»). Цифра 0 в індексі, що позначає, що відтинається відрізок нескінченної довжини, відповідає паралельному розташуванню грані щодо даної осі; куб, наприклад, складається із шести граней: (100), (010), (001) (100), ( ВІД), (001). Сукупність усіх граней, що утворюють ту або іншу ферму, позначається індексом однієї із цих граней: наприклад, куб — єт» форма {100} кубічної сингонії, октаєдр — форма {111}.
Індекси для тригональних і гексагональних кристалів, для котври$ використовується система чотирьох кристалографічні всієї, полягають аз чотирьох цифр; третя цифра не є, конеч-.
але, незалежної: величина відрізка, що відтинається на третій горизонтальній осі, визначається відрізками по двом іншим осям, і в результаті сума перших трьох цифр у таких індексах завжди дорівнює нулю. Одиничними площинами в цьому записі можна вважати площини (1011) або (1121).