. Тригональна сингонія включає всі кристали, що мають одну потрійну вісь
Гексагональна сингонія включає всі кристали, що мають одну гексагональну вісь (вісь 6-го порядку).
Тетрагональна сингонія включає всі кристали, що мають одну четверную (тетрагональну) вісь (вісь 4-го порядку).
Кубічна (правильна, ізометрична) сингонія включає всі кристали, що мають чотири потрійні й три четверние осі. Потрійні осі паралельні діагоналям куба й нахилено одна до іншої під кутом 70°32.
(Іноді тригональна сингонія вважається частиною гексагональної сингонії, так що в цьому випадку налічується всього шість різних сингоній.).
Кристали різних сингоній (систем) у свою чергу діляться на види (класи) симетрії по сукупності елементів симетрії, які доповнюють характерні елементи сингонії, зазначені вище. Існує 32 виду симетрії, але багато хто з них мають дуже невелике значення й рідке зустрічаються серед мі-
неральних утворів. У кожній сингонії гнітюче чис-,ло відомих представників виявляє ступінь симетрій! максимально можливу для даної сингонії: вони належать до так званого голоєдрическому виду симетрії даної сингонії. Тут нам необхідно згадати всі голоєдрические й тільки трохи інших видів симетрії, у які попадають найважливіші дорогоцінні мінерали
I. Триклннная сингонія. Голоєдрический класа пинако-идальний. Єдиний елемент симетрії — центр симетрії. Загальна форма — пинакоид; оскільки кожна форма полягає
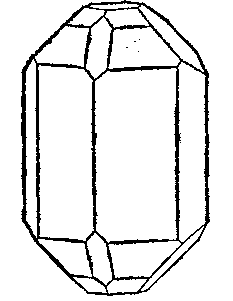
Рис. 22. Кристал топазу
Рис, 23. Ромбоедр,.
з пари паралельних граней, у реальних кристалах повинне існувати не менше трьох таких форм. Цей вид симетрії виражений у плагіоклазах, кіаніті й родоніті
II.
Моноклінна сингонія. Голоєдрический клас, призматичний. Елементи симетрії: 1 подвійна вісь, 1 площина ( під прямим кутом до осі) і центр симетрії
Особливі форми — різні види пинакоидов, загальна форма — призма. Приблизно половина всіх відомих кристалічних речовин ставиться до цього класу, а серед ювелірних матеріалів — ортоклаз (мал. 3), сподумен, євклаз, сфен і епідот (мал. 20).
III.
Ромбічна сингонія. Голоєдрический клас: ромбоби-пирамидальний. Елементи симетрії: 3 взаємно перпендикулярні подвійні осі, 3 площини ( під прямим кутом до осей) і центр симетрії
Особливі форми — пинакоиди й призми; загальна форма — бипирамида. За значенням цей клас займає друге меето. До нього належать топаз (мал. 22), олівін і хризоберил, а також менш відомі мінерали: андалузит, кордиерит, бериллонит, гамір-бергит, данбурит, брукит, фіброліт, корнерупин, єнетатит і цоизит.
IV.
Тетрагональна сингонія. Голоєдрический класа дитетра-гон-бипирамидальний. Елементи симетрії: 1 тетрагональна вісь і 4 подвійні осі, перпендикулярні їй, 5 площин симетрії (иод прямим кутом до всіх осей) і центр симетрії
Є велика кількість особливих форм; довільно розташована грань повторюється у вигляді чотирьох пар граней навколо четверной осі, а вони відбиваються симетрично в нижній частині кристала, утворюючи, таким чином, дитетрагональную бипирамиду. Прикладами мінералів цього класу служать циркон (мал. 2), каситерит і везувіан
Тетрагон-Бипирамидалишй клас. Елементи симетрії: 1 тетрагональна вісь, 1 площина ( під прямим кутом до осі) і центр симетрії
Особливі форми — пинакоид (, що розбудовується із граней, розташованих під прямим кутом до осі 4-го порядку) і тетрагональні призми ( із граней, паралельних цієї осі); загальна форма в цьому випадку — 8-гранная тетрагональна бипирамида без тих площин симетрії, що проходять через тетрагональну вісь, які створюють дитетрагональную симетрію й характерні для голоєдрии. До цього класу ставиться скаполіт, якому іноді надають огранювання дорогоцінного каменю
V.
Гексагональна сингонія. Голоєдрический класу дигекса-гон-бипирамидальний. Елементи симетрії: 1 гексагональна вісь, 6 подвійних осей ( під прямим кутом до осі 6-го порядку), 7 площин симетрії й центр симетрії
Цей клас — гексагональний аналог голоєдрического класу тетрагональної сингонії. Серед особливих форм фігурують пина-коиди, призми й гексагональні бипирамиди; загальна форма має 6 пара граней, що симетрично повторюються, що приводить до утвору дигексагональной бипирамиди. Видатним представником цього класу є берилл.
Гексагон-Бипирамидалъний клас. Елементи симетрії: 1 вісь 6-го порядку, 1 площина ( під прямим кутом до осі) і центр симетрії
Прикладом мінералів цього класу служить, як уже вказувалося, апатит (мал. 18).
VI.
Тригональна сингонія. Голоєдрический клас: дитригон-скаленоєдрический. Елементи симетрії: 1 потрійна вісь, 3 подвійні осі, перпендикулярні потрійний осі, 3 площини ( під прямим кутом до подвійних осей) і центр симетрії
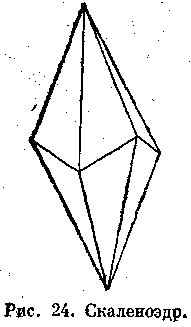
Є ряд особливих форм, у тому числі ромбоедри (мал. 23). Загальна форма, у якій відсутня горизонтальна площина симетрії,- скаленоєдр, а не бипирамида; його назва походить від слова scalene (разносторонний, косою) — по вигляду нерівносторонніх трикутних граней (мал. 24). Приклади мінералів цього класу — корунд, кальцит і гематит
Дитригон-Пирамидалъний клас. Елементи симетрії: 1 потрійна вісь і 3 пересічні по ній площини
Особливі форми включають як тригональні, так і гексагональні призми, так що кристали можуть мати поперечний переріз у вигляді рівностороннього трикутника. У них немає центру симетрії, загальна форма — піраміда (але не бипирамида). Різні кінці кристала мають різну симетрію. Найбільш наочним прикладом мінералів цього класу є турмалін (мал. £).
Трйгон-Шрапецоєдрический клас. Елементи симетрії: 1 потрійна вісь і 3 подвійні осі, перпендикулярні потрійний осі
Площин симетрії ні, і в кристалах цього класу проявляється єнантиоморфизм: їх загальні форми мають праву й ліву модифікації, симетричний^-симетричні-дзеркально-симетричні й нееовмещающиеся. До цього класу ставиться Кварц (мал. 11), що володіє дивною властивістю обертання площини поляризації (уперше відкритим Араго); ця властивість характерна для кристалів, Позбавлених площин симетрії
Дитригон-Бипирамидалъний клас. Елементи симетрії: 1 потрійна вісь; 3 подвійні осі під прямим кутом до неї; 3 площини, кожна з яких містить потрійну вісь і одну з подвійних осей, і 1 площина, перпендикулярна потрійний осі
Єдиним представником цього класу серед мінералів є рідкий дорогоцінний бенитоит.
Ромбоєдрический клас. Елементи симетрії: 1 потрійна вісь і центр симетрії
Особливі форми: пинакоиди й гексагональні призми. Загальна форма — ромбоедр. До цього класу ставляться фенакіт, диоп-таз і виллемит.
VII. Кубічна сингонія. Голоєдрический клас: сорокавось-мигранники. Елементи симетрії: 3 осі 4-го порядку, 4 потрійні осі, 6 подвійних осей; 3 площини, розташовані під прямим кутом до осей 4-го порядку; 6 інших площин (перпендикулярних подвійним осям), центр симетрії
З особливих форм для всіх видів симетрії кубічної сингонії типові куб і ромбододекаєдр. Серед інших особливих форм
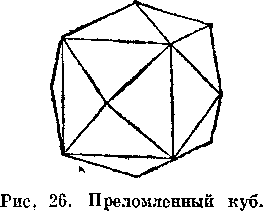
цього класу — октаєдр (мал. 25), переломлений куб (мал. 26), икоситетраєдри й переломлений октаєдр (мал. 27). У кристалах алмаза іноді чітко видна 48-гранная загальна форма ( сорока-восьмигранник) (мал. 28). Іншими прикладами мінералів цього класу служать гранат, шпінель і флюорит
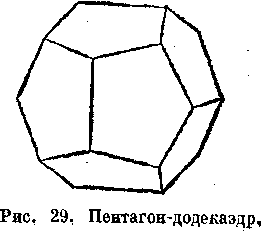
Дидодекаєдрический клас. Елементи симетрії: 3 подвійні осі, 4 потрійні осі, 3 площини ( під прямим кутом до подвійних осей) і центр симетрії
Характерна особлива форма — пентагон-додекаєдр (мал. 29), іноді називаний пиритоєдром, тому що він часто добре виражений у піриті — одному з головних представників цього класу
Клас тетраедра. Елементи симетрії: 3 подвійні осі, 4 потрійні осі, 6 площин
Центру симетрії ні, характерна особлива форма — тетраедр (мал. 5), Прикладом мінералів цього класу служить сфалерит